1.DFS—深度优先搜索

排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式 共一行，包含一个整数 n。

输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围

1
1≤n≤7

输入样例：

1
3

输出样例：

1
2
3
4
5
6
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

「完整代码：」

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;
const  int N = 10;
int n;
int path[N];
bool st[N];
void dfs(int x)
{
    // 如果x到达最后一层，就进行输出
    if(x == n)
    {
        for(int i = 0; i < n;i++)
        {
            cout << path[i] + 1 << " ";
        }
        cout << endl;
        return;
    }
    
    for(int i = 0; i < n;i++)
    {
        if(!st[i]) {
            path[x] = i;
            st[i] = true;
            dfs(x+1);
            st[i] = false;
            
        }
    } 
}
int  main()
{   
    
    cin >> n;
    dfs(0);
    return  0;
}

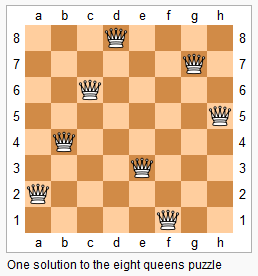
n皇后问题

n−皇后问题是指将 n个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

1_597ec77c49-8-queens.png

现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式
共一行，包含整数 n。

输出格式
每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围
1≤n≤9
输入样例：

1
4

输出样例：

1
2
3
4
5
6
7
8
9
10
11
.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..


「解决思路：」

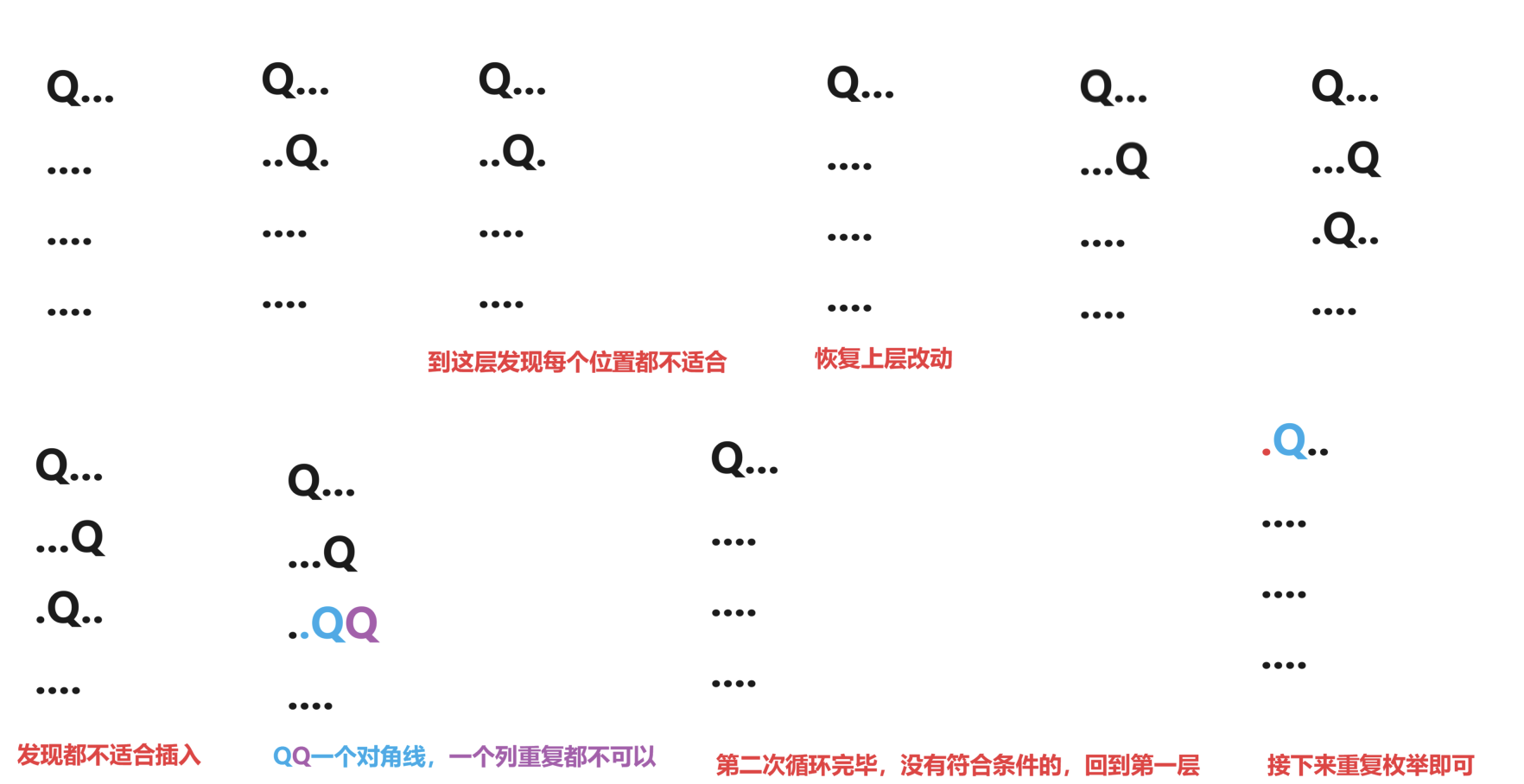
我们可以利用深搜，一行一行来解决，每一行里面的每一列都可以试着枚举一下设置为Q，然后此点的两条对角线设置为true已使用，此列设置为已使用，之后在遍历下一行。

如果遇到某一行没有符合条件的，即这一层for循环调用完毕后，没有触发if函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for(int i = 0; i < n;i++)
    {
        if(!col[i] and !dg[u+i] and !udg[u-i+n])
        {
            arr[u][i] = 'Q';
            col[i] = true;
            dg[u+i] = true;
            udg[u - i +n] = true;
            dfs(u+1);
            col[i] = false;
            dg[u+i] = false;
            udg[u - i +n] = false;
            arr[u][i] = '.';
        }
    }

然后本层dfs运行结束后,回溯到上层调用的地方，说明此路不通，恢复上一层改动

1
2
3
4
5
dfs(u+1);
		col[i] = false;
      dg[u+i] = false;
      udg[u - i +n] = false;
      arr[u][i] = '.';

然后继续for循环判断下一个位置是否可以改为‘Q’，继续判断，直到找出结果。

「图解：」

image-20240131102332864

「完整代码：」

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <bits/stdc++.h>
using namespace std;
const int N = 20;

char g[N][N];
bool col[N], dg[N], udg[N];
int n;
void dfs(int u)
{
    if (u == n)
    {
        for (int i = 0; i < n; i++)
        {
            cout << g[i] << endl;
        }
        cout << endl;
        return;
    }

    for (int i = 0; i < n; i++)
    {
        if (!col[i] and !dg[u + i] and !udg[u - i + n])
        {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[u - i + n] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[u - i + n] = false;
            g[u][i] = '.';
        }
    }
}

int main()
{

    cin >> n;

    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            g[i][j] = '.';
        }
    }
    dfs(0);

    return 0;
}

2.BFS—广度优先搜索

迷宫问题

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1、 表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1)处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m)处，至少需要移动多少次。

数据保证 (1,1)处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

输入格式第一行包含两个整数 n和 m。

接下来 n 行，每行包含 m 个整数（0 或 1 ），表示完整的二维数组迷宫。

输出格式
输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围
1≤n,m≤100
输入样例：

1
2
3
4
5
6
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

1
8

「解题思路：」

此题从起点开始，每次向四周（上下左右）扩散，在没个点的位置上记录起点到这个点的距离，之后遍历完成后，输出右下角的距离值，此题完成。

「变量介绍：」

1
2
3
4
5
6
7
8
9
10
using ll = long long;
using PII = pair<int, int>;  // 因为是二维数组，存下每个点需要pair类型
// 走迷宫
const int N = 105; // 矩阵最大数
int n, m; // 对应题目的 n m
int g[N][N]; // 存储地图
int d[N][N]; // 存储每个点到起点的距离

// 队列 存储下一步能走到的所有点，包含四周方向
queue<PII> q;

「函数详解：」

此题核心！！！！！！！！！！！

对于此题的路径就是按图中所示，如果旁边的点不为1可以走，那么则会把四周的依次填入队列中，并且把距离数组d中相应的该点加上前面路径的距离。

1
2
3
4
5
if(x >= 0 and y >= 0 and x < n and y < m and g[x][y] == 0 and d[x][y] == -1)  // 这里的if要判断附近的点是否被之前的路径走过，走过则不会覆盖，没走过则覆盖，求出最短路。
          {
              d[x][y] = d[t.first][t.second] + 1;
              q.push({x,y});
          }

对于附近的点，则使用偏移向量进行更新，每次循环四次，加上偏移量，则对应上下左右。

1
2
3
4
5
6
 int dx[4] = {-1, 0, 1, 0};
 int dy[4] = {0, 1, 0, -1};

// 进行偏移叠加
int x = t.first + dx[i];
int y = t.second + dy[i];

「路径变化：」

image-20240125231248533

「队列变化：」

image-20240126002502292

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int dfs()
{
    q.push({0, 0});
    memset(d, -1, sizeof d);
    d[0][0] = 0;

    int dx[4] = {-1, 0, 1, 0};
    int dy[4] = {0, 1, 0, -1};

    while (!q.empty())
    {
        auto t = q.front();
        q.pop();
        for(int i = 0; i < 4;i++)
        {
            int x = t.first + dx[i];
            int y = t.second + dy[i];

            if(x >= 0 and y >= 0 and x < n and y < m and g[x][y] == 0 and d[x][y] == -1)
            {
                d[x][y] = d[t.first][t.second] + 1;
                q.push({x,y});
            }
        }
    }

    return d[n-1][m-1];
}

「完整代码：」

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using PII = pair<int, int>;
// 走迷宫
const int N = 105;
int n, m;
int g[N][N]; // 存储地图
int d[N][N]; // 存储每个点到起点的距离

// 队列 存储下一步能走到的点，包含四周方向
queue<PII> q;

int dfs()
{
    q.push({0, 0});
    memset(d, -1, sizeof d);
    d[0][0] = 0;

    int dx[4] = {-1, 0, 1, 0};
    int dy[4] = {0, 1, 0, -1};

    while (!q.empty())
    {
        auto t = q.front();
        q.pop();
        for(int i = 0; i < 4;i++)
        {
            int x = t.first + dx[i];
            int y = t.second + dy[i];

            if(x >= 0 and y >= 0 and x < n and y < m and g[x][y] == 0 and d[x][y] == -1)
            {
                d[x][y] = d[t.first][t.second] + 1;
                q.push({x,y});
            }
        }
    }

    return d[n-1][m-1];
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cin >> g[i][j];


    cout << dfs() << endl;
    return 0;
}

八段码

在一个 3×33×3 的网格中，1∼81∼8 这 88 个数字和一个 x 恰好不重不漏地分布在这 3×33×3 的网格中。

例如：

1
2
3
1 2 3
x 4 6
7 5 8

在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1
2
3
1 2 3
4 5 6
7 8 x

例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1
2
3
1 2 3   1 2 3   1 2 3   1 2 3
x 4 6   4 x 6   4 5 6   4 5 6
7 5 8   7 5 8   7 x 8   7 8 x

现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

输入格式

输入占一行，将 3×33×3 的初始网格描绘出来。

例如，如果初始网格如下所示：

1
2
3
1 2 3 
x 4 6 
7 5 8

则输入为：1 2 3 x 4 6 7 5 8

输出格式

输出占一行，包含一个整数，表示最少交换次数。

如果不存在解决方案，则输出 −1−1。

输入样例：

1
2 3 4 1 5 x 7 6 8

输出样例

1
2
19

「解题思路：」

典型的求最短路问题，可以使用BFS

可以 利用一维数组转为二维数组的方式巧妙解决本题

先求出 x 原本的一维数组坐标，然后利用以下代码进行转为二维坐标

1
2
3
4
5
6
// 要找到 x 字符所在的下标
   int index_x = front_str.find('x');
   // 进行坐标转换
   // x对应在 二维坐标轴的 坐标
   int double_x = index_x / 3;
   int double_y = index_x % 3;

之后在 x 的二维坐标基础上上下左右移动，求出对应的二维坐标，再将四个上下左右进行转为一维坐标，交换x与其上下左右的值，如果之前没出现过交换后的字符串的状态，进行次数加一。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
for (int i = 0; i < 4; i++)
        {
            // 上下左右对应的坐标
            int two_a = double_x + dx[i];
            int two_b = double_y + dy[i];
            // 保证数组不越界
            if (two_a < 3 and two_a >= 0 and two_b < 3 and two_b >= 0)
            {
                // 然后 推回 一维数组坐标
                int one_ab = two_a * 3 + two_b;
                swap(temp_str[index_x], temp_str[one_ab]);

                if (!d.count(temp_str))
                {
                    q.push(temp_str);
                    d[temp_str] = d[front_str] + 1;
                }
                // 最后别忘了位置还原
                swap(temp_str[index_x], temp_str[one_ab]);
            }
        }

「变量介绍：」

1
2
3
4

const string end_str = "12345678x"; // 最终的目的字符串
unordered_map<string, int> d; // 存储 每个字符串最短形成次数的数组
queue<string> q;    // bfs常用的队列

「完整代码：」

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <bits/stdc++.h>
using namespace std;


const string end_str = "12345678x"; // 最终的目的字符串
unordered_map<string, int> d; // 存储 每个字符串最短形成次数的数组
queue<string> q;    // bfs常用的队列

int bfs(string start_str)
{
    d[start_str] = 0; // 初始状态的距离设置为0
    int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, 1, -1};

    q.push(start_str);

    while (!q.empty())
    {
        string front_str = q.front();
        string temp_str = front_str;
        if (temp_str == end_str)
            return d[temp_str];
        q.pop();
        // 要找到 x 字符所在的下标
        int index_x = front_str.find('x');
        // 进行坐标转换
        // x对应在 二维坐标轴的 坐标
        int double_x = index_x / 3;
        int double_y = index_x % 3;

        for (int i = 0; i < 4; i++)
        {
            // 上下左右对应的坐标
            int two_a = double_x + dx[i];
            int two_b = double_y + dy[i];
            // 保证数组不越界
            if (two_a < 3 and two_a >= 0 and two_b < 3 and two_b >= 0)
            {
                // 然后 推回 一维数组坐标
                int one_ab = two_a * 3 + two_b;
                swap(temp_str[index_x], temp_str[one_ab]);

                if (!d.count(temp_str))
                {
                    q.push(temp_str);
                    d[temp_str] = d[front_str] + 1;
                }
                // 最后别忘了位置还原
                swap(temp_str[index_x], temp_str[one_ab]);
            }
        }
    }

    return -1;
}
int main()
{
    string s1;

    for (int i = 0; i < 9; i++)
    {
        char c1;
        cin >> c1;
        s1 += c1;
    }

    int res = bfs(s1);

    cout << res << endl;
    return 0;
}