1.两两交换链表中的节点
引用:代码随想录 (programmercarl.com)
力扣题目链接
建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
初始时,cur指向虚拟头结点,然后进行如下三步:
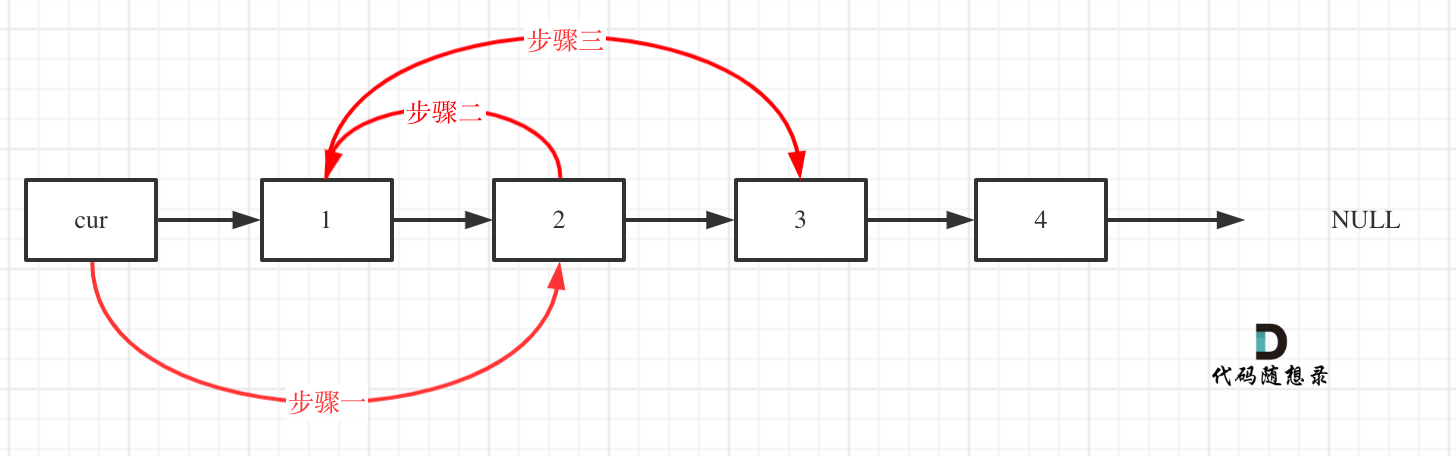
操作之后,链表如下:
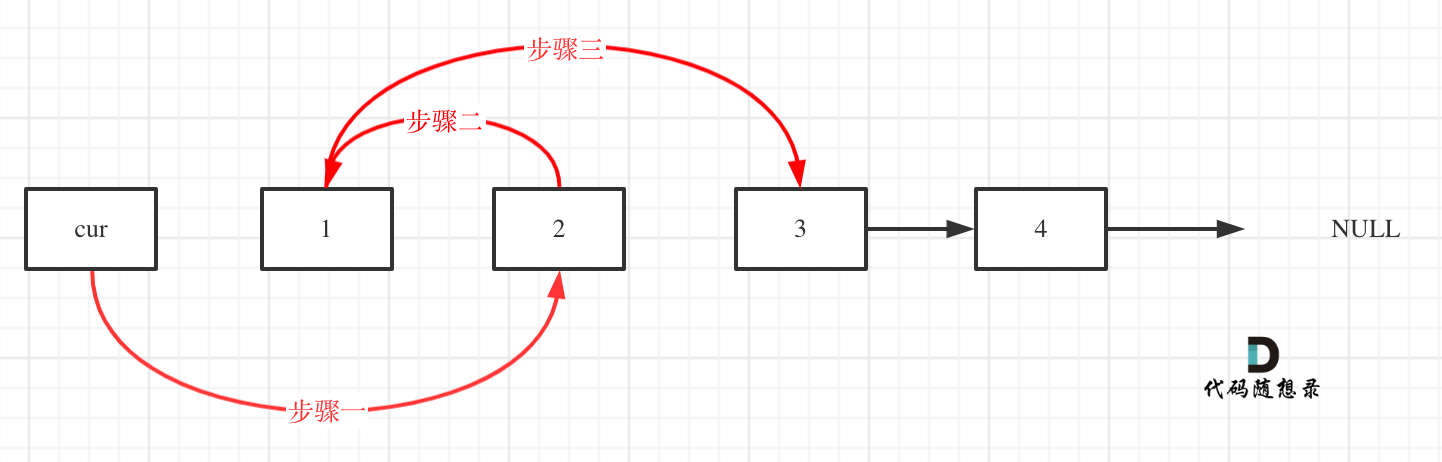
看这个可能就更直观一些了:
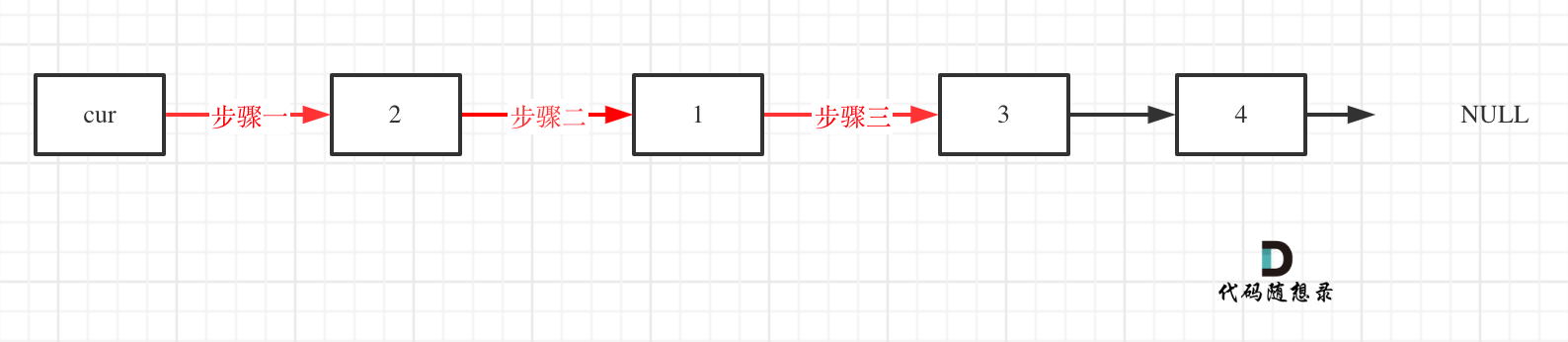
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr) {
ListNode* tmp = cur->next;
ListNode* tmp1 = cur->next->next->next;
cur->next = cur->next->next;
cur->next->next = tmp;
cur->next->next->next = tmp1;
cur = cur->next->next;
}
return dummyHead->next;
}
};
|
2.删除链表的倒数第N个节点
「思路:」先让快指针走 n+1步,之后让快慢指针同时走,直到快指针等于NULL,为什么是n+1呢,因为删除倒数第n一个节点需要前一个(即n-1)节点的信息,所以让快指针多走一步。
参考:代码随想录 (programmercarl.com)
- 定义fast指针和slow指针,初始值为虚拟头结点,如图:
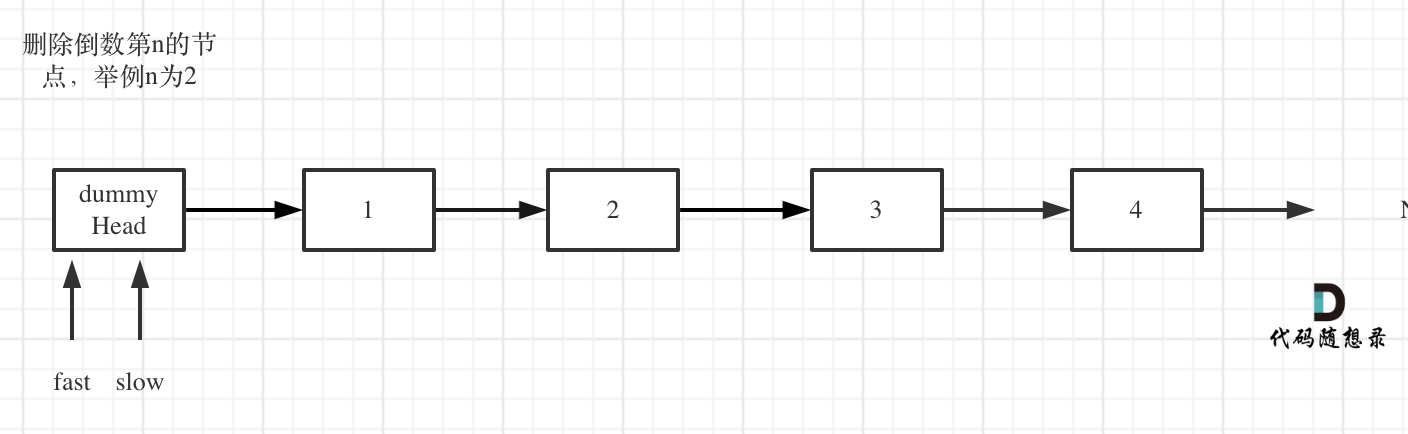
- fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
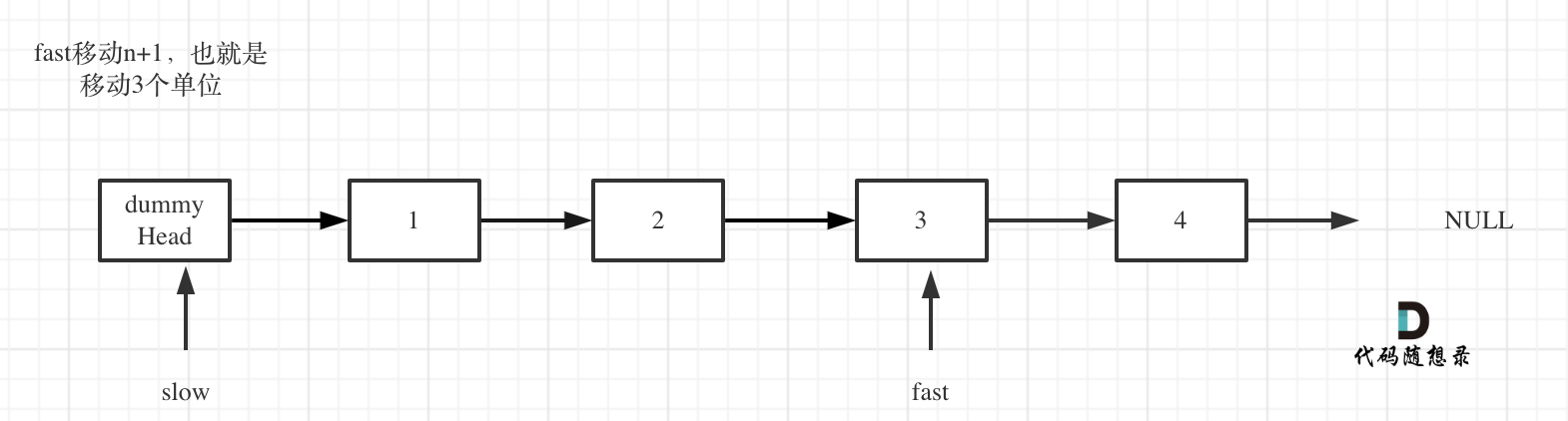
- fast和slow同时移动,直到fast指向末尾,如题:
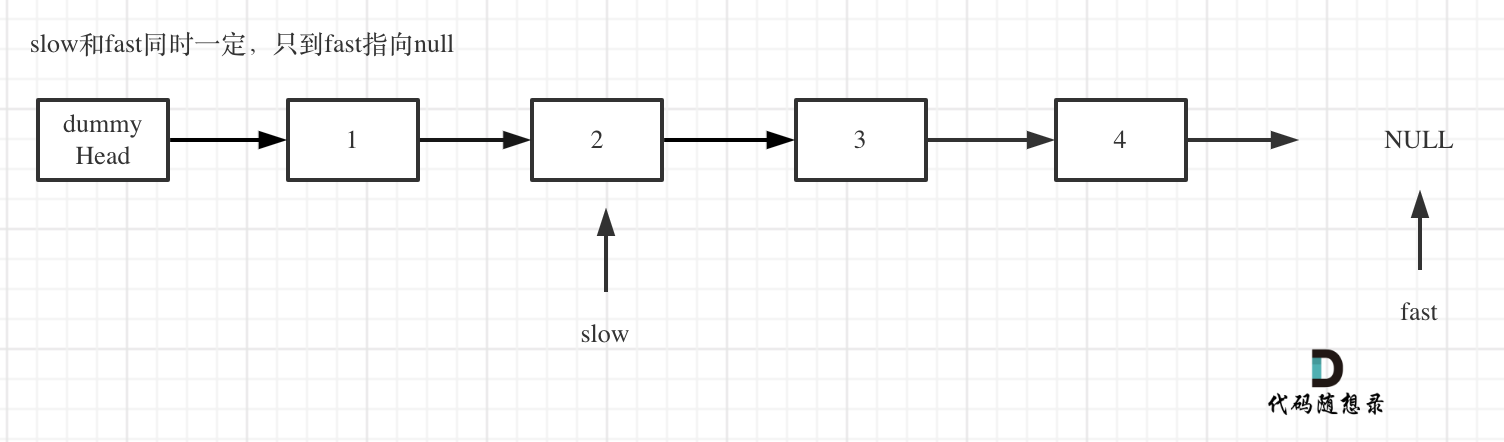
- 删除slow指向的下一个节点,如图:
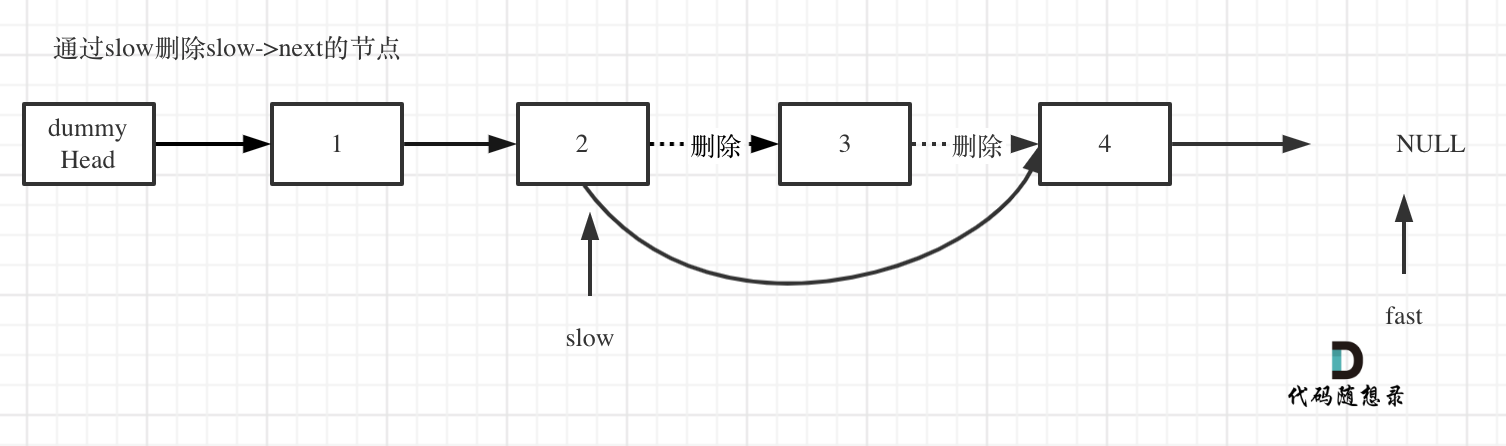
此时不难写出如下C++代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* slow = dummyHead;
ListNode* fast = dummyHead;
while(n-- && fast != NULL) {
fast = fast->next;
}
fast = fast->next;
while (fast != NULL) {
fast = fast->next;
slow = slow->next;
}
slow->next = slow->next->next;
return dummyHead->next;
}
};
|
3.链表相交
面试题 02.07. 链表相交 - 力扣(LeetCode)
「重点:」这个题是指针相等,而不是值相等
「解决思路:」
- 遍历两个链表,计算长度,算出差值
- 让长的链表头指针先移动,对齐短的指针

- 再依次遍历后面的指针,查到相等返回 curA,否则返回NULL
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode * tmpA = headA;
ListNode * tmpB = headB;
int lenA = 0,lenB = 0;
while(tmpA != NULL) {
lenA++;
tmpA = tmpA -> next;
}
while(tmpB != NULL) {
lenB++;
tmpB = tmpB -> next;
}
tmpA = headA;
tmpB = headB;
if(lenB > lenA) {
swap(lenB,lenA);
swap(tmpB,tmpA);
}
int charZhi = lenA - lenB;
while(charZhi--) {
tmpA = tmpA -> next;
}
while(tmpA != tmpB) {
tmpA = tmpA -> next;
tmpB = tmpB -> next;
}
if(tmpA != NULL) {
return tmpA;
} else {
return NULL;
}
}
};
|
4.环形链表II
力扣题目链接
4.1 解法1:存下走过的节点地址,进行对比查找
「思路:」遍历链表,存储每个节点的指针,先存储,再往下跳,之后再遍历数组是否存在此指针,存在说明找到了环的入口,返回当前节点。
「优缺点:」
- 优点:容易理解,思路简单暴力
- 缺点:时间复杂度偏高
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode * tmp = head;
vector<ListNode *> arr;
while(tmp != NULL) {
arr.push_back(tmp);
tmp = tmp -> next;
if(find(arr.begin(),arr.end(),tmp) != arr.end()) {
break;
}
}
return tmp;
}
};
|
4.2 解法2:快慢双指针思路
「思路:」
参考:代码随想录 (programmercarl.com)
快指针fast一次走两步,慢指针slow一次走一步,显然如果有环,快指针一定会追上慢指针。

找到相遇点之后,要找到环的入口位置。
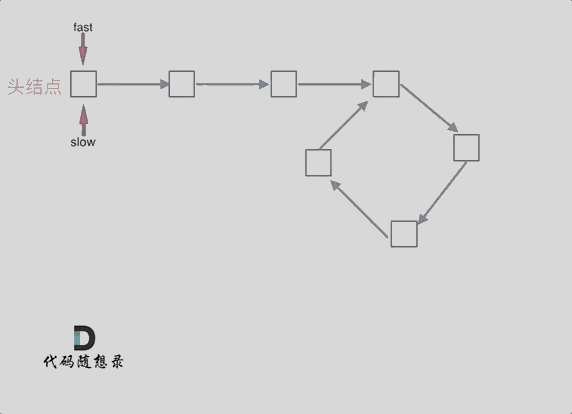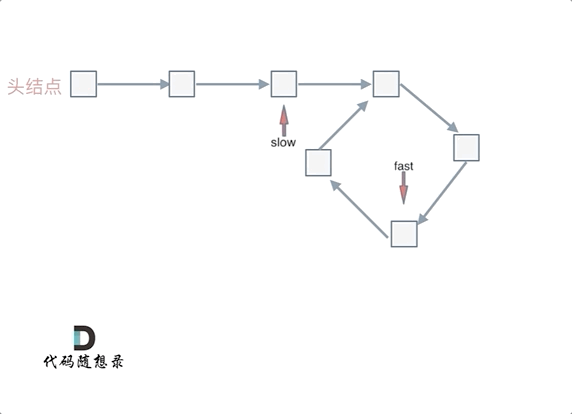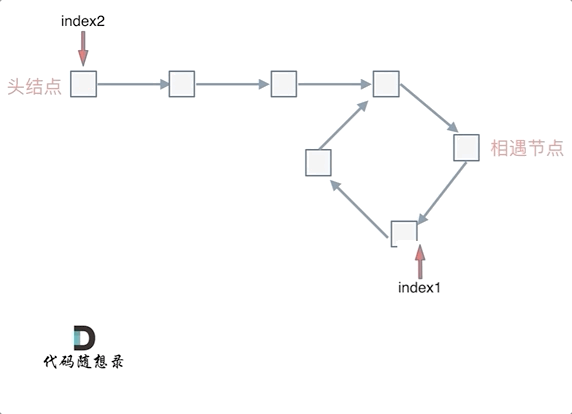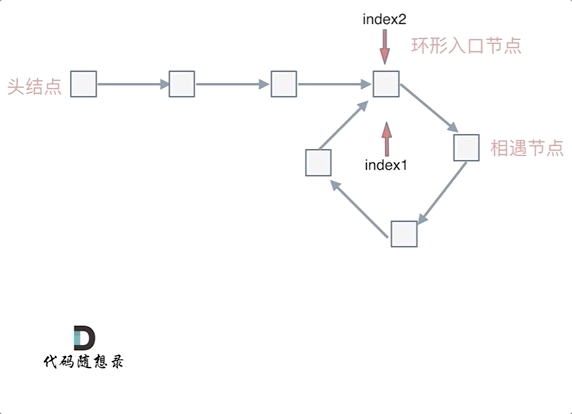
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示:

fast与slow相遇时,slow走过的步数 为 ==x + y== ,fast 走过的步数为 ==x + n(y + z)==
n表示转过的圈数。
因为 fast 走两步,slow走一步,时间一定时,慢指针要达到快指针的步数则需要变为两倍。
可得: ==2(x + y )=x+n(y+z)==
即而 推出: ==x = n(y+z) - y==
整理可得: ==x = (n-1)(y+z) +z==
因为 n圈数肯定大于等于1,可以想象在操场跑步的两人,快的人追慢的人,必然要跑完一圈,则 n >= 1
所以 当 n = 1时,推出 ==x = z==
即当找到相遇点后,让 fast(index1) 与 head(index2) 同时一步一步走,最终相遇的点就是入口。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode * fast = head;
ListNode * slow = head;
while(fast != NULL and fast -> next != NULL) {
slow = slow->next;
fast= fast->next -> next;
if(slow == fast) {
ListNode * index1 = fast;
ListNode * index2 = head;
while(index1 != index2) {
index1 = index1 -> next;
index2 = index2 -> next;
}
return index1;
}
}
return NULL;
}
};
|



















