1.排序

1.快速排序

快速排序利用了递归的思想。
定义头指针，如果头指针对应的数 < arr[mid]，l++，直到遇到大于等于 num的数。
定义尾指针，如果尾指针对应的数 > arr[mid],r–，直到遇到小于等于num的数。
当双方各遇到不符合条件的停止循环，进行数值交换。
每一轮循环会把路径上遇到的大于 arr[mid]的数放到右边，小于的放左边。
最后再次分置，再次递归以上过程，最后遇到两个元素的组合（再往下递归，l = r，直接停止），假如是

元素 1 3

下标 4 5

mid取4，arr[mid] 为 1，头指针不满足 < 1的条件，则l不动；

尾指针满足 > 1的条件，尾指针 –，然后头尾相等，结束循环；

实际顺序不变，因为就是小到大。

元素 3 1

下标 4 5

加入为 3 ，1

头指针不满足 < 1，尾指针不满足 >1，且满足头 < 尾，则交换元素。

元素	1	3
下标	4	5

元素	3	1
下标	4	5

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int arr[N];

void qucik_sort(int arr[],int l,int r)
{
    if (l >= r) return;
    
    int num_mid = arr[(l + r ) / 2], i = l - 1,j = r + 1;
    
    while(i < j) 
    {
        do i++;while(arr[i] < num_mid);
        do j--;while(arr[j] > num_mid);
    
        if(i < j) swap(arr[i],arr[j]);
    }
    
    qucik_sort(arr,l,j);
    qucik_sort(arr,j+1,r);
    

}
int main()
{
    int n;cin >> n;
    for(int i = 1; i <= n;++i) 
    {
        cin >> arr[i];
    }
    
    qucik_sort(arr,1,n);
    
    for(int i =1; i <= n;++i) 
    {
        cout << arr[i] << " ";
    
    }
}

2.归并排序

归并排序更加体现了递归的思想。
「思路：」假设有两个已经排好顺序（小到大）的数组A，B，然后依次从第一位开始比较，如果Ai小于Bj，则往tmp临时数组里添加Ai，然后Ai的指针移向下一个，Bj不动，再次比较，直到其中一个数组走到尽头，再依次扫尾，把剩下的元素添加进tmp临时数组，再把临时数组的结果赋值给原数组。
「注意：」这里注意，必须必须最后再把临时数组的元素依次赋值给原数组，因为原数组是拆分开来递归向上返回再次运算的，如果不把排好序的结果赋值给原数组，再向上递归会出错。
「解题步骤：」
先利用递归将数组分割成单独元素的每一个部分，最少是两个元素互相比较。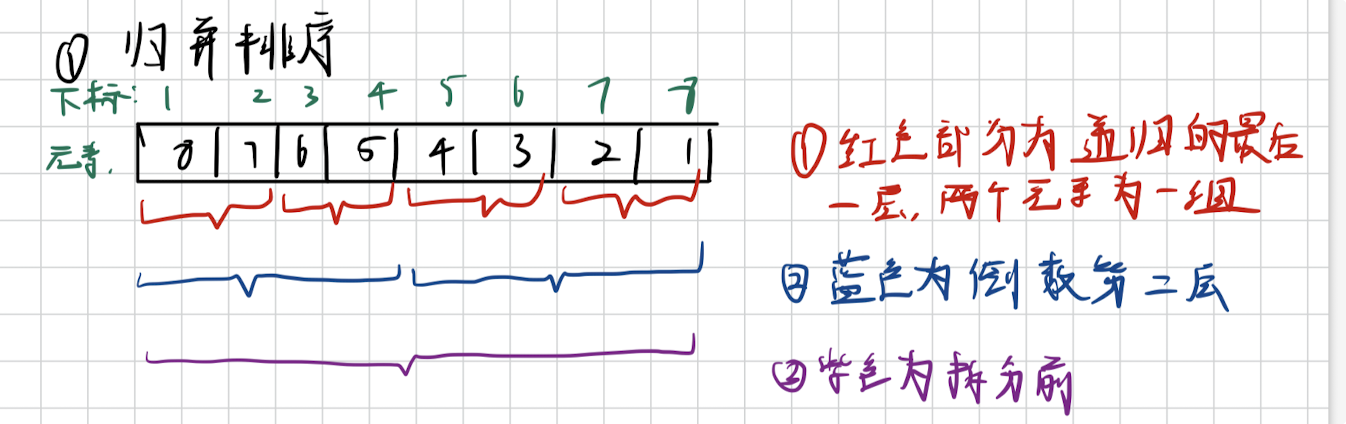
之后互相比较，更新tmp，赋值给原数组
同理接下来一样，依次完成运算，向上递归。注意一定要赋值给原数组。

2.二分查找

1.查找左边界

arr 数组，num为要查找的数，l 数组起点，r数组终点，需要查找的值num默认为 3。
数组默认是从小到大有序排列
「查找左边界」：即数组分为两个部分：一是 >= num的部分，而是 < num的部分。
例如图中所示
「取数组mid」：
第一次取值： mid = （1+6）/ 2 = 3, mid取值为3，arr[mid] >= num,则需要求得的左边界一定在 [l,mid]之间，因为是取num的左边界，则令 r = mid，因为条件为>= ，r是有可能取到边界的。
接下来再进行一次循环判断，则mid = 2，arr[mid] < num，则所选范围一定在 (mid,r] （左开右闭）内，所以令 l = mid +1。
接下来 l == r，循环终止，找到了第一个 >= num 的下标，即左边界。
如果数组内无num，即无输入的需要查找的元素，则 l的返回值为第一个 > num的元素下标值

「代码如下：」

int getLeft(int arr[],int num,int l,int r) 
{
    if (l >= r) return 0;
    
    
    while(l < r) 
    {   
        int mid = (l + r) / 2;
        if(arr[mid] >= num) 
        {
            r = mid;
        } else 
        {
            l = mid + 1;
        }
    }
    return l;
}

2.查找右边界

arr 数组，num为要查找的数，l 数组起点，r数组终点, 需要查找的值num默认为 3。
数组默认是从小到大有序排列
「查找右边界」：即数组分为两个部分：一是 <=num 的部分，而是 > num的部分。
例如图中所示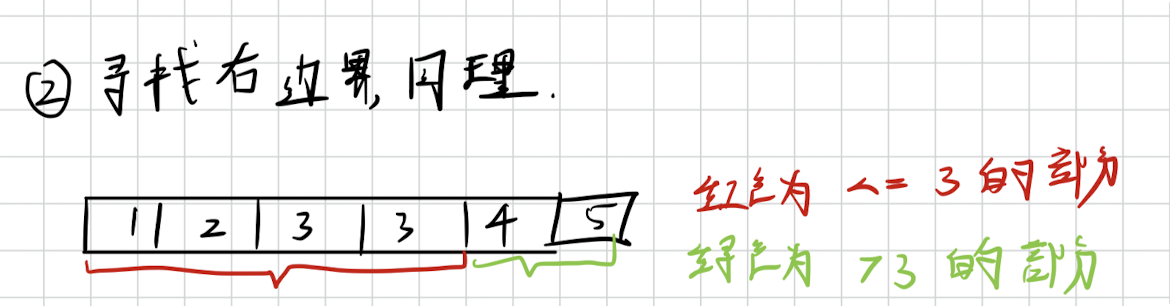
「取数组mid」：
第一次取值： mid = （1+6）/ 2 = 3, mid取值为3，arr[mid] <= num ,则需要求得的左边界一定在 [mid,r]之间，因为是取num的右边界，则令 l = mid ，因为条件为 <= ，l 是有可能取到边界的。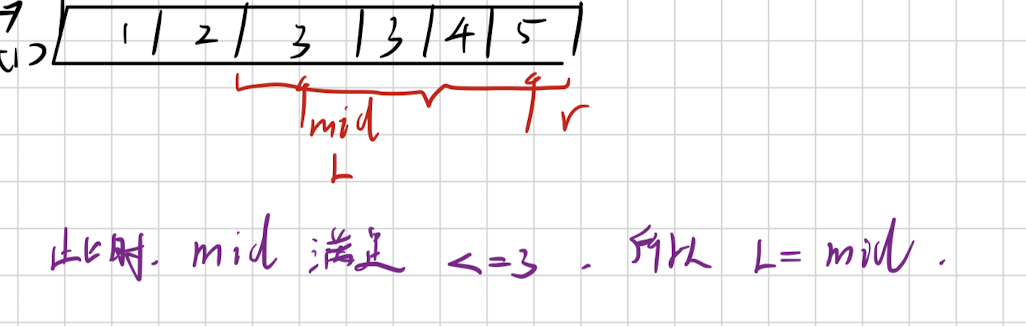
接下来再进行一次循环判断，则mid = 4，arr[mid] <= num，则所选范围一定在 [mid,r] （左闭右闭）内，所以令 l = mid +1。
之后下一次循环，mid = （4+6 ）/ 2 = 5， arr[mid] > num,不满足条件，则令 r = mid - 1，因为当前mid肯定不符合范围，直接取下一个。
接下来 l == r，循环终止，找到了最后一个 <= num 的下标，即右边界。
如果数组内无num，即无输入的需要查找的元素，则 l的返回值为第一个 < num的元素下标值

「代码如下：」

int getRight(int arr[],int num,int l,int r) 
{
    if( l >= r ) return 0;
    
    while(l < r) 
    {
        int mid = (l + r + 1) / 2;
        if(arr[mid] <= num) 
        {
            l = mid;
        } else 
        {
            r = mid - 1;
        }
     }
     
     return l;
}

3.例题数的范围

789. 数的范围 - AcWing题库

「完整代码：」

#include<bits/stdc++.h>
using namespace std;
const int N =  100000+10;
int arr[N];

int getLeft(int arr[],int num,int l,int r) 
{
    if (l >= r) return 0;
    
    
    while(l < r) 
    {   
        int mid = (l + r) / 2;
        if(arr[mid] >= num) 
        {
            r = mid;
        } else 
        {
            l = mid + 1;
        }
    }
    return l;
}

int getRight(int arr[],int num,int l,int r) 
{
    if( l >= r ) return 0;
    
    while(l < r) 
    {
        int mid = (l + r + 1) / 2;
        if(arr[mid] <= num) 
        {
            l = mid;
        } else 
        {
            r = mid - 1;
        }
     }
     
     return l;
}
int main() 
{
    int n,q;
    cin >> n >> q;
    for(int i = 1; i <= n;++i) 
    {
        cin >> arr[i];
    }
    
    for(int i = 0; i < q;++i) 
    {
        
        int num;cin >> num;
        int left = getLeft(arr,num,1,n);
        

        int right = getRight(arr,num,1,n);
        
        cout << left-1 << " " << right -1<< "\n";
    }
    return 0;
}

4.例题数的三次方根

790. 数的三次方根 - AcWing题库

#include <bits/stdc++.h>
using namespace std;
int main()
{
    double x;
    cin >> x;
    double l = -10000, r = 10000;
    while( r - l > 1e-8)
    {
        double mid = (l + r) / 2;
        if(mid * mid * mid >= x) 
        {
            r = mid;
        } else {
            l = mid;
        }
    }
    cout <<  fixed << setprecision(6) << l  << "\n";
}

1.排序

1.快速排序

2.归并排序

2.二分查找

1.查找左边界

2.查找右边界

3.例题 数的范围

4.例题 数的三次方根

3.例题数的范围

4.例题数的三次方根