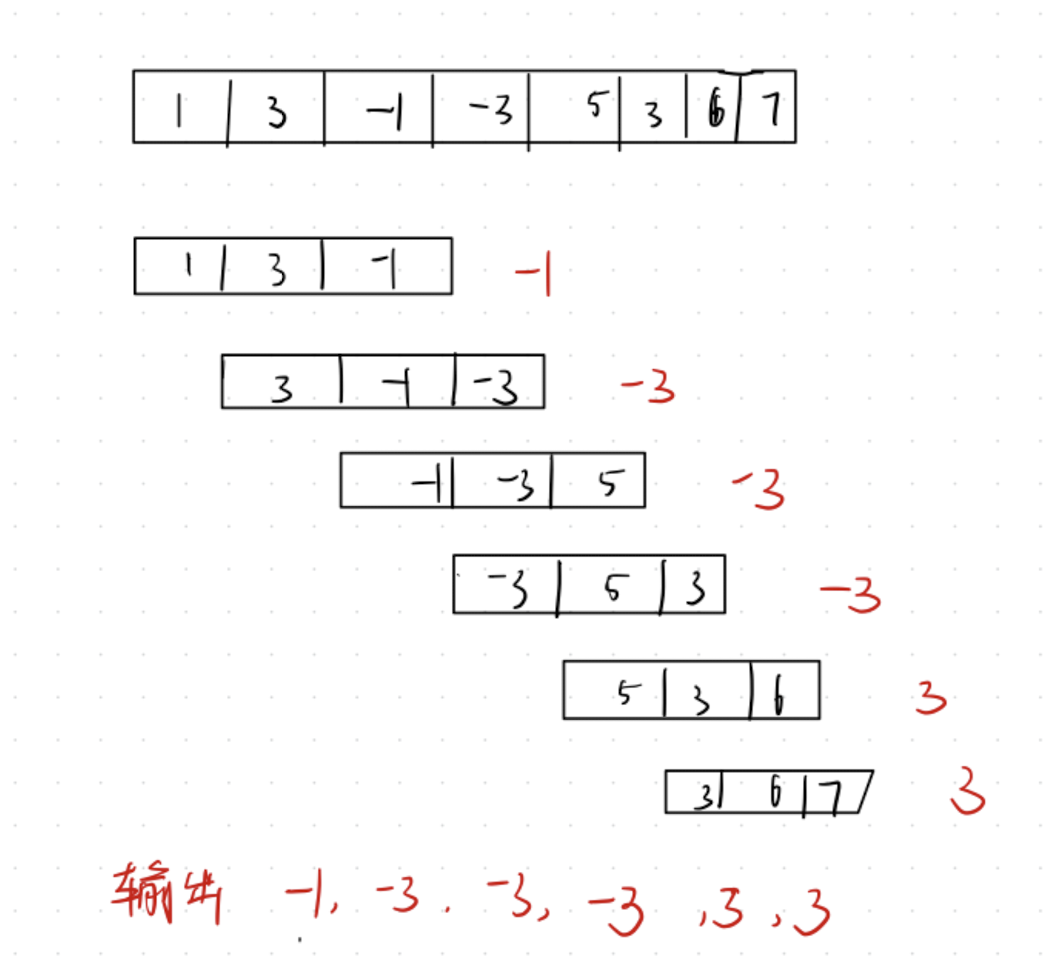
1.滑动窗口

「实现思路：」

  1. 滑动窗口可以用对列实现，k 就对应队列的长度，最朴素的方式是使用暴力枚举，但是时间复杂度较高。

  2. 降低时间复杂度则可以使用单调队列，那么什么是单调队列呢？

    单调队列：假设我们要求的一块区域为3的最小值，那么我们在数组循环的时候，让队头默认最小值，而且对列里的数必须是单调递增，因为只有这样，才能保证队头最小，每次不用循环枚举浪费多余时间，直接输出区域内最小值。

「变量介绍：」

1
2
3
const int N = 1e6 + 10;  
int arr[N]; // 这是存储所有元素的数组集合
int k_arr[N]; // 这是单调对列，存储的是元素的下标值，要获取值 则 通过 arr[k_arr[x]] 获取对应值。

「具体做法：」

  1. 每次循环，先判断当前队列是否超出 k 的长度，超出则让单调对列的头指针后移一位。

  2. 然后再判断当前元素 x 与单调队列的尾元素的大小关系。

    x > 单调队列[end] ：就让x 的下标添加进队尾。

    x > 单调队列[end]：就让单调对列的队尾弹出，在循环进行判断大小关系，直到队尾 < x元素或者队为空，再把元素进行添加。

  3. 如果是循环 i 满足了 k 的长度要求，就可以进行输出队头，上述操作已经保证是 队头是该区域的最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 获取最小值做法  
for(int i = 1; i <= n;i++)
    {
     		// 判断是否需要移动单调队列的头指针
        if(hh <= tt and k_arr[hh] < i - k  + 1) hh++;
				// 当队尾针对应的值 大于等于 x，则需要弹出队尾，直接 t--，之后再填写覆盖就好
        while(hh <= tt and arr[k_arr[tt]] >= arr[i])
        {
            tt--;
        }
     		// 重新填入元素
        k_arr[++tt] = i;
				// 输出队头
        if(i >= k ) cout 	<< arr[k_arr[hh]] << " ";
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
// 获取最大值做法----同理
for(int i = 1;i <= n;i++)
   {
       if(hh <= tt and k_arr[hh] < i - k + 1) hh++;
       while(hh <=tt and arr[k_arr[tt]] <= arr[i]) 
       {
           tt--;
       }
       k_arr[++tt] = i;

       if(i >= k) cout << arr[k_arr[hh]] << " ";

   }

「完整代码：」

题目链接：154. 滑动窗口 - AcWing题库

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;
int arr[N];
int k_arr[N];

int main()
{

    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
    {
        cin >> arr[i];
    }
    
    int hh = 1,tt = 0;
    for(int i = 1; i <= n;i++)
    {
        if(hh <= tt and k_arr[hh] < i - k  + 1) hh++;

        while(hh <= tt and arr[k_arr[tt]] >= arr[i])
        {
            tt--;
        }
        k_arr[++tt] = i;

        if(i >= k ) cout << arr[k_arr[hh]] << " ";
    }
    hh = 1,tt = 0;
    cout << endl;
    for(int i = 1;i <= n;i++)
    {
        if(hh <= tt and k_arr[hh] < i - k + 1) hh++;
        while(hh <=tt and arr[k_arr[tt]] <= arr[i]) 
        {
            tt--;
        }
        k_arr[++tt] = i;

        if(i >= k) cout << arr[k_arr[hh]] << " ";

    }
    return 0;
}