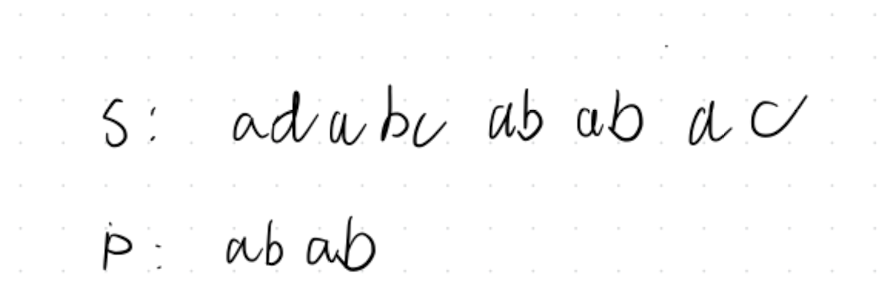1.kmp 字符串匹配
「kmp算法介绍:」
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) [1]。
字符串的模式匹配是一种常用的运算。所谓模式匹配,可以简单地理解为在目标(字符串)中寻找一个给定的模式(也是字符串),返回目标和模式匹配的第一个子串的首字符位置。通常目标串比较大,而模式串则比较短小。
简洁来说,就是在较长的字符串S中寻找子串P是否存在以及多少个的问题。
「实现思路:」
朴素做法:可以使用暴力枚举,但是时间复杂度高,耗时。
优化做法:使用ne[]数组存储子串P最大匹配后缀与最匹配大前缀的下标。
如果遇到不匹配,则跳到P子串与当前位置元素匹配的最大前缀位置。
这么说可能很抽象,画图表示。
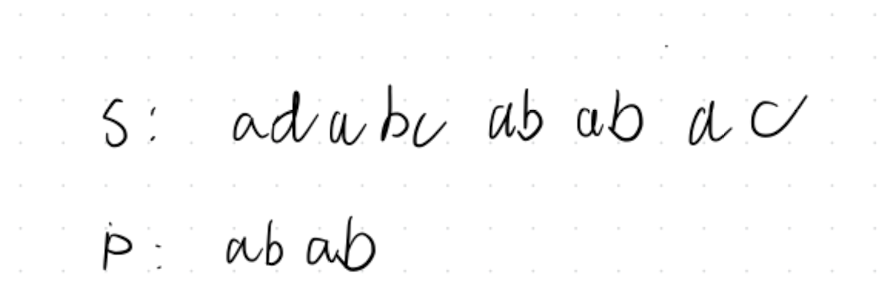
假如以上 S (长传)与 P(子串)
先让P匹配自己,让每一位都能找到与自己相符的最大前缀与后缀的位置。
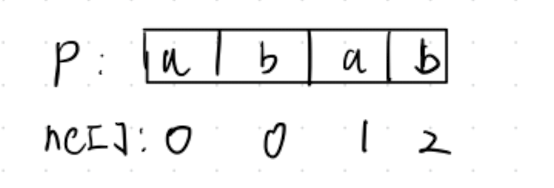
为什么要统计出ne数组呢?
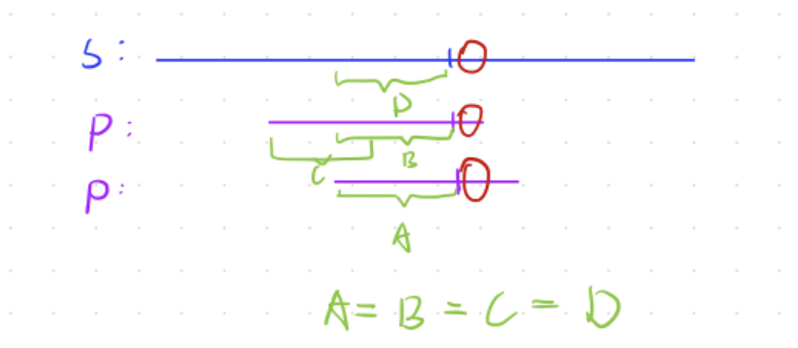
假如S与P在红点处不匹配,那么p需要往后移动进行匹配,在暴力做法中,当然可以一个一个匹配,但是太浪费时间。
通过图示,可以清楚看到,P进行移动,是可以直接移动到B == A(图中绿色括号)的位置,既然B=A,那么C=B,所以得出结论
A=B=C,即匹配不通过的点的前一个位置的最大前缀下标(可以理解为前缀长度)。
例如上图abab,当最后一个b不匹配时,前一个对应的是1,即跳到前面a的位置,形成了如下表格关系,再接着比对
|
|
|
不匹配位置 |
|
|
| a |
b |
a |
c |
|
|
| a |
b |
a |
b |
|
|
|
|
a |
b |
a |
b |
「实现函数:」
ne数组:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
for(int i = 2,j = 0 ; i <= n;i++)
{
while (j and P[i] != P[j+1])
{
j = ne[j];
}
if(P[i] == P[j+1])
{
j++;
}
ne[i] = j;
}
|
匹配函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
for(int i = 1,j = 0;i <= m;i++)
{
while(j and S[i] != P[j+1])
{
j = ne[j];
}
if(S[i] == P[j+1])
{
j++;
}
if(j == n)
{
cout << i - n << endl;
j = ne[j];
}
}
|
「完整代码:」
题目链接:https://www.acwing.com/problem/content/833/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include <bits/stdc++.h>
using namespace std;
const int M = 1e6+10;
const int N = 1e5 +10;
char P[N];
char S[M];
int ne[N];
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n,m;
cin >> n;
cin >> (P + 1);
cin >> m;
cin >> (S + 1);
for(int i = 2,j = 0 ; i <= n;i++)
{
while (j and P[i] != P[j+1])
{
j = ne[j];
}
if(P[i] == P[j+1])
{
j++;
}
ne[i] = j;
}
for(int i = 1,j = 0;i <= m;i++)
{
while(j and S[i] != P[j+1])
{
j = ne[j];
}
if(S[i] == P[j+1])
{
j++;
}
if(j == n)
{
cout << i - n <<" ";
j = ne[j];
}
}
return 0;
}
|
2.「更新—–哈希解法:」
详细讲解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
const int M = 1e6 + 10, p = 131;
char P[M];
char S[M];
ULL P_h[M], S_h[M], h_P[M], h_S[M];
ULL getP(int l, int r)
{
return h_P[r] - h_P[l - 1] * P_h[r - l + 1];
}
ULL getS(int l, int r)
{
return h_S[r] - h_S[l - 1] * S_h[r - l + 1];
}
int main()
{
int n, m;
cin >> n >> P + 1;
cin >> m >> S + 1;
P_h[0] = 1;
S_h[0] = 1;
for (int i = 1; i <= n; i++)
{
P_h[i] = P_h[i - 1] * p;
h_P[i] = h_P[i - 1] * p + P[i];
}
for (int i = 1; i <= m; i++)
{
S_h[i] = S_h[i - 1] * p;
h_S[i] = h_S[i - 1] * p + S[i];
}
ULL p_hx = getP(1, n);
for (int i = 1, j = n; j <= m; j++, i++)
{
if (getS(i, j) == p_hx)
{
cout << i - 1 << " ";
}
else
{
continue;
}
}
return 0;
}
|